This topic takes on average 55 minutes to read.
There are a number of interactive features in this resource:
 Science
Science
The chi-squared test is performed on observed data that we want to compare to expected values, such as frequency data on how many colours of tulip are found in a flower shop. These expected values can be either data from a previous observation, or as in the example below, simply of equal proportion.
We want to investigate whether there is a preferred colour of tulip found in a local flower shop. Our ‘expected values’ would simply be that there are an equal number of each surveyed colour, and it is this that we are comparing our observed values against. Our null hypothesis states ‘there is no difference in the frequency of each colour of tulip in the flower shop’.
| Tulip colour | Expected value | Observed value |
| Pink | 20 | 17 |
| Purple | 20 | 13 |
| Red | 20 | 32 |
| White | 20 | 12 |
| Yellow | 20 | 26 |
| Total | 100 | 100 |
The first step is to calculate the difference between the expected and the observed values for each of the colours of tulip, and subsequently square them.
| Tulip colour | Expected value | Observed value | d | d2 |
| Pink | 20 | 17 | -3 | 9 |
| Purple | 20 | 13 | -7 | 49 |
| Red | 20 | 32 | 12 | 144 |
| White | 20 | 12 | -8 | 64 |
| Yellow | 20 | 26 | 6 | 36 |
The formula for the calculation of the chi-squared test statistic (χ2) is as follows:
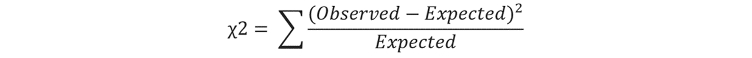
We can input our data into this formula:
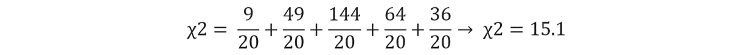
Now we have our test-statistic, we can compare this to a critical value table using our significance level and our degrees of freedom (this is equal to the sample size subtracted by 1, which in this case would be 4).
Our test-statistic of 15.1 is greater than the critical value of 9.49 at p = 0.05 with 4 degrees of freedom, therefore this suggests that there is a statistically significant difference between the observed frequency of each colour of tulip in the flower shop, and the expected frequency. Therefore, we can reject our null hypothesis.

Flower frequency at the florists